Understanding the Circle A Foundation for Radius Exploration

Before delving into methods for calculating the radius, let’s solidify our understanding of the circle itself. A circle is a perfect two-dimensional shape with every point on its boundary equidistant from a fixed point called the center. This defining characteristic, the radius, is the key to unlocking various circle-related calculations.

Unveiling the Radius: Four Proven Approaches

Now, equipped with a clear understanding of the circle’s structure, let’s explore four effective methods for finding the radius:

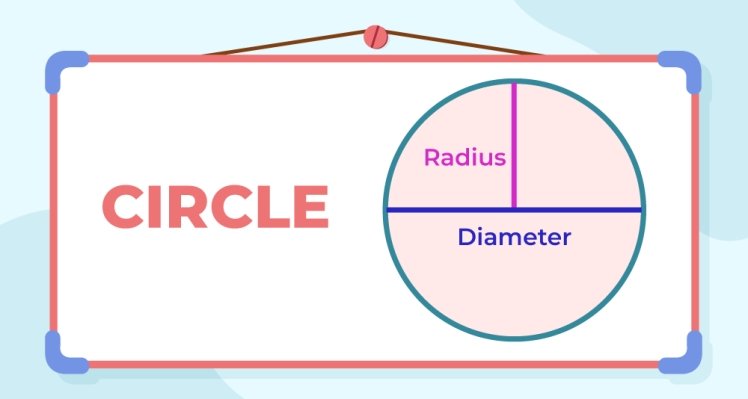
1. The Diameter’s Embrace: Divide and Conquer

• Relationship:The diameter, denoted by “d,” is the longest straight line segment passing through the center, dividing the circle into two equal halves.
• Radius (r) = Diameter (d) / 2 is the formula.
• Example:If the diameter is 12 centimeters, then the radius is 12 cm / 2 = 6 centimeters.

Prompt: Imagine a pizza with a diameter of 30 centimeters. What is the length of a radius connecting the center to a point on the crust? (Answer: 15 centimeters)

2. The Circumference’s Embrace: A Wrap-Around Measurement

• Relationship:The circumference, denoted by “c,” is the total distance around the circle’s edge.
• Radius (r) = Circumference (c) / (2 * π) is the formula.
• Note:Remember π (pi) is the mathematical constant approximately equal to 3.14159.
• Example:If the circumference of a bicycle wheel is 200 centimeters, then the radius is 200 cm / (2 * 3.14159) ≈ 31.83 centimeters.

Prompt: A hula hoop has a circumference of 2 meters. How long is a radius from the center to the rim? (Answer: 2 m / (2 * 3.14159) ≈ 0.3183 meters)

3. The Area’s Whisper: A Measure of Enclosed Space

• Relationship:The area, denoted by “A,” represents the amount of space enclosed within the circle’s boundary.
• Radius (r) = √(Area (A) / π is the formula.
• Example:If the area of a pond is 400 square meters, then the radius is √(400 m² / 3.14159) ≈ 11.31 meters.

Prompt: A 100 square foot circular gardening patch. What is the radius from the center to the edge? (Answer: √(100 ft² / 3.14159) ≈ 5.64 feet)

4. The Intersecting Chords: Unveiling Secrets with Geometry

• Concept:By strategically drawing chords within the circle, you can create geometric relationships that reveal the radius.
• Example:Draw a diameter and a chord intersecting at a right angle inside the circle. The radius forms the hypotenuse of a right triangle, and using Pythagorean theorem (a² + b² = c²) or other geometric properties, you can solve for the radius.

Prompt: Draw a diameter and a chord intersecting at a right angle in a circle. If the diameter is 16 centimeters and the chord is 12 centimeters, what is the radius? (Requires application of Pythagorean theorem)

Beyond Formulas: Visualizing and Applying Radius

Radius isn’t just about calculations; it’s a crucial concept in various real-world applications:

• Engineering:Designing gears, bearings, and other circular components requires accurate radius calculations.
• Construction:Building arches, bridges, and other curved structures demands understanding of radii.
• Art and Design:Creating circular patterns, logos, and other artistic elements often involves using radii.
• Science:Studying planetary orbits, cell structures, and other circular phenomena necessitates radius concepts.

Remember: The choice of method depends on the information you have available. If you know the diameter, use the first method. If you know the circumference, use the second. If you know the area, use the third. And if you have geometric information about intersecting lines, use the fourth method.

By understanding these methods and the essence of the radius, you’ll be well-equipped to tackle various circle-related problems with confidence.